1. Theory
A cursory introduction to theory and concepts related to electrochemical impedance spectroscopy is presented herein. For a more thorough and complete study, the reader is encouraged to consult academic textbooks and the scientific literature1-23.
Experimental electrochemistry can be as powerful as it is tricky. Even simple DC methods (e.g., voltammetry, open circuit potential, chronoamperometry, chronopotentiometry) are often plagued by inaccuracies and/or poor signal-to-noise ratios resulting from seemingly insignificant or overlooked sources. Variables that can affect electrochemical data include, but are not limited to: the state and quality of electrodes, electrolyte, experimental hardware, the physical laboratory layout, software experimental parameters, arrangement of cables, and grounding configuration.
AC techniques, like electrochemical impedance spectroscopy (EIS), can be similarly affected by these variables and sources of error. The user must exercise particular care and caution when setting up and running EIS experiments as the impact of small sources of error often has a larger effect on data quality than for DC methods. Obtaining and interpreting meaningful EIS data, as with many other facets of electrochemistry, requires repeated practice and often some trial-and-error with respect to both the hardware and software.
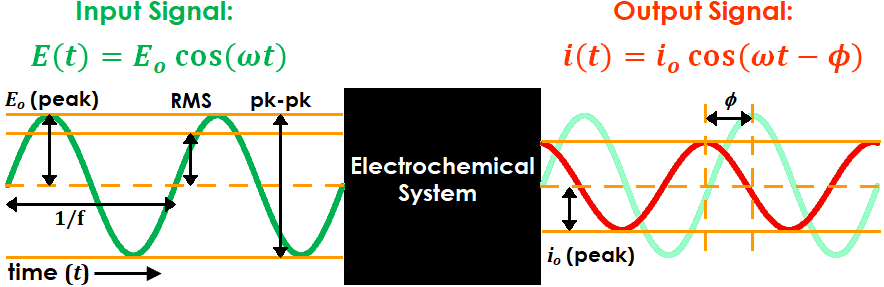
In AC electrochemistry, a sinusoidal potential (or current) signal is applied to a system and the resulting current (or potential) signal is recorded and analyzed (see Figure 1 for diagram and Table 1 for associated terminology). The frequency and amplitude of the input signal are tuned by the user, while the output signal normally has the same frequency as the input signal but its phase may be shifted by a finite amount.
Practically, frequency () is reported in units of Hz. However, for mathematical convenience the angular frequency (
), which has units of rad/s and is equivalent to
, is typically used for calculations instead (e.g., see input and output signal equations in Figure 1). Similarly, the phase angle (
) is typically reported in units of degrees but calculated in units of radians.
There are three conventions often used to define the input (and sometimes output) signal amplitude: peak, peak-to-peak, and RMS. “Peak” refers to the difference between the sine wave set point (i.e., the potential or current at the beginning of the sine wave period) and its maximum or minimum point (i.e., the potential or current at one quarter of the sine wave period). “Peak-to-peak” is simply twice the peak value (see Figure 1).
“RMS”, which stands for “root mean square”, is a mathematical quantity used primarily in electrical engineering to compare AC and DC voltages or currents. Though its practical relevance and importance to EIS measurements is somewhat minimal, it is still widely used in the industry to characterize input signal amplitude. Mathematically, it is equivalent to the peak value divided by , or roughly peak times 0.707 (see Figure 1).
During an EIS experiment, a sequence of sinusoidal potential signals with varying frequencies, but similar amplitudes, is applied to an electrochemical system. Typically, frequencies of each input signal are equally spaced on a descending logarithmic scale from ~10 kHz – 1 MHz to a lower limit of ~10 mHz – 1 Hz. Application of these input and output signals is usually performed automatically via a potentiostat/galvanostat.
Monitoring the progress of an EIS experiment can be done by observing the input and output signals on a single current vs. potential graph called a Lissajous plot (see Figure 2). Depending on the system under study, as well as the applied frequency and amplitude, the shape of the resulting Lissajous plot may vary. Throughout an EIS experiment, the user can observe the progression and pattern of Lissajous plots as a means of identifying possibly erroneous data.
The shape of the current vs. potential Lissajous plot for a stable, linear electrochemical system typically appears as either a tilted oval or straight line that repeatedly traces over itself (see Figure 2). The shape of the oval reveals the magnitude of the phase angle. For example, if the Lissajous plot looks like a perfect circle, it means the output signal is +90° or -90° out of phase. This is also the EIS response experienced by an ideal capacitor or inductor. If the Lissajous plot looks like a straight line tilted toward right, then the output signal is completely in phase with the input signal. If the straight line is tilted toward left, then the output signal is completely out of phase (+/-180°) with respect to the input signal.
2. References
- Orazem, M. E.; Tribollet, B. Electrochemical impedance spectroscopy, 2nd ed. John Wiley & Sons, Inc.: Hoboken, NJ, 2017.
- Lasia, A. Electrochemical Impedance Spectroscopy and its Applications Springer New York: New York, NY, 2014.
- Jorcin, J.; Pébère, N.; Tribollet, B. CPE analysis by local electrochemical impedance spectroscopy. Electrochim. Acta, 2006, 51(8-9), 1473–1479.
- Hirschorn, B.; Orazem, M. E.; Tribollet, B.; Vivier, V.; Frateur, I.; Musiani, M. Determination of effective capacitance and film thickness from constant-phase-element parameters. Electrochim. Acta, 2010, 55(21), 6218–6227.
- Roy, S. K.; Orazem, M. E.; Tribollet, B. Interpretation of Low-Frequency Inductive Loops in PEM Fuel Cells. Journal of The Electrochemical Society, 2007, 154(12), B1378.
- Orazem, M.; Durbha, M.; Deslouis, C.; Takenouti, H.; Tribollet, B. Influence of surface phenomena on the impedance response of a rotating disk electrode. Electrochim. Acta, 1999, 44(24), 4403–4412.
- Orazem, M. E.; Agarwal, P.; Jansen, A. N.; Wojcik, P. T.; Garcia-Rubio, L. H. Development of physico-chemical models for electrochemical impedance spectroscopy. Electrochim. Acta, 1993, 38(14), 1903–1911.
- Remita, E.; Boughrara, D.; Tribollet, B.; Vivier, V.; Sutter, E.; Ropital, F.; Kittel, J. Diffusion Impedance in a Thin-Layer Cell: Experimental and Theoretical Study on a Large-Disk Electrode. The Journal of Physical Chemistry C, 2008, 112(12), 4626–4634.
- Huang, V. M.; Wu, S.; Orazem, M. E.; Pébère, N.; Tribollet, B.; Vivier, V. Local electrochemical impedance spectroscopy: A review and some recent developments. Electrochim. Acta, 2011, 56(23), 8048–8057.
- Macdonald, D. D. Review of mechanistic analysis by electrochemical impedance spectroscopy. Electrochim. Acta, 1990, 35(10), 1509–1525.
- Macdonald, D. D. Reflections on the history of electrochemical impedance spectroscopy. Electrochim. Acta, 2006, 51(8-9), 1376–1388.
- Macdonald, D. D. Some Advantages and Pitfalls of Electrochemical Impedance Spectroscopy. CORROSION, 1990, 46(3), 229–242.
- Barsoukov, E.; Macdonald, J. R. Impedance spectroscopy: theory, experiment, and applications, 2nd ed. Wiley.
- Bertoluzzi, L.; Bisquert, J. Equivalent Circuit of Electrons and Holes in Thin Semiconductor Films for Photoelectrochemical Water Splitting Applications. The Journal of Physical Chemistry Letters, 2012, 3(17), 2517–2522.
- Bisquert, J. Influence of the boundaries in the impedance of porous film electrodes. PCCP, 2000, 2(18), 4185–4192.
- Bisquert, J. Theory of the Impedance of Electron Diffusion and Recombination in a Thin Layer. The Journal of Physical Chemistry B, 2002, 106(2), 325–333.
- Yuan, X.; Song, C.; Wang, H.; Zhang, J. Electrochemical Impedance Spectroscopy in PEM Fuel Cells Springer London: London, 2010.
- Agarwal, P.; Orazem, M. E.; Garcia‐Rubio, L. H. Measurement Models for Electrochemical Impedance Spectroscopy. Journal of The Electrochemical Society, 1992, 139(7), 1917.
- Agarwal, P.; Orazem, M. E.; Garcia‐Rubio, L. H. Application of Measurement Models to Impedance Spectroscopy. Journal of The Electrochemical Society, 1995, 142(12), 4159.
- Macdonald, D. D.; Urquidi‐Macdonald, M. Application of Kramers-Kronig Transforms in the Analysis of Electrochemical Systems. Journal of The Electrochemical Society, 1985, 132(10), 2316.
- Urquidi-Macdonald, M.; Real, S.; Macdonald, D. D. Application of Kramers-Kronig Transforms in the Analysis of Electrochemical Impedance Data. Journal of The Electrochemical Society, 1986, 133(10), 2018.
- Boukamp, B.; Macdonald, J. R. Alternatives to Kronig-Kramers transformation and testing, and estimation of distributions. Solid State Ionics, 1994, 74(1-2), 85–101.
- Boukamp, B. A. A Linear Kronig-Kramers Transform Test for Immittance Data Validation. Journal of The Electrochemical Society, 1995, 142(6), 1885.